Biografía:
Eratóstenes era de Cirene, capital de la Cirenaica, que en la actualidad está en Libia (Shahhat). Nació en
Eratóstenes además fue muy conocido, y tuvo mochos rivales, por eso se le conoció también como el “beta”, refiriéndose a que no era bueno en nada, aunque sabía de todo. Esto era porque Eratóstenes cultivó muchas ramas de la ciencia: matemáticas, poesía, geografía, astronomía y la filosofía. Otros en cambio le llamaban el pentatlón, campeón de cinco disciplinas, aunque ninguna fuese olímpica.
Además de todo ello, Eratóstenes fue el tercer director de Alejandría, y fue nombrado por Ptolomeo Evergetes. Duró en ese privilegiado puesto durante cuarenta y un años. Lamentablemente no nos ha llegado mucha información sobre él porque se quemaron la mayoría de sus obras, lo que si sabemos es que fue capaz de medir la medida de la circunferencia terrestre, cuya experiencia explicaremos posteriormente. Eratóstenes murió en el año
Experiencia:
Para poder explicar bien los procedimientos de Eratóstenes, hay que tener cierta base de geografía y astronomía:
La tierra está divida por unos ejes cartesianos, denominados paralelos (y) y meridianos (x), para facilitar la descripción de un punto en la superficie. Hay que conocer que los paralelos más importantes son: ecuador (0º), trópico de Cáncer (23,5º Norte), trópico de Capricornio (23,5º Sur), círculo Polar Ártico (66,5º Norte) y círculo Polar Antártico (66,5º Sur). Mientras que el meridiano más importante es el de Greenwich que marca los 0º.

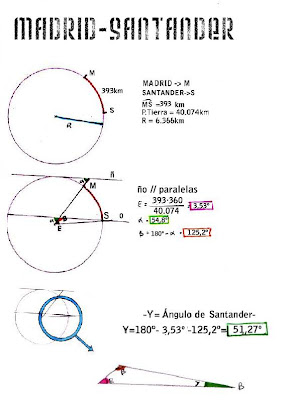
Estos gráficos seguramente clarifiquen los conceptos:
 A Eratóstenes le llegó la noticia de que había un lugar en el que el sol en un día del año se reflejaba en los pozos, lo cual no podía sino significar que estaba muy cerca del trópico de Cáncer (que para él no existía pero sabía que los rayos incidían perpendicularmente) y se le ocurrió que podía medir la circunferencia terrestre, lo único que necesitaba era saber que distancia había entre Alejandría y Asuán
A Eratóstenes le llegó la noticia de que había un lugar en el que el sol en un día del año se reflejaba en los pozos, lo cual no podía sino significar que estaba muy cerca del trópico de Cáncer (que para él no existía pero sabía que los rayos incidían perpendicularmente) y se le ocurrió que podía medir la circunferencia terrestre, lo único que necesitaba era saber que distancia había entre Alejandría y Asuán (que por cierto están en el mismo meridiano), el dichoso lugar. Después de obtener una medida un tanto inexacta todo fue coser y cantar, calculó el ángulo que formaban los rayos de sol con una estaca el mismo día y a la misma hora (7,2º), y por una sencilla regla de tres calculó la superficie
(que por cierto están en el mismo meridiano), el dichoso lugar. Después de obtener una medida un tanto inexacta todo fue coser y cantar, calculó el ángulo que formaban los rayos de sol con una estaca el mismo día y a la misma hora (7,2º), y por una sencilla regla de tres calculó la superficieterrestre con un porcentaje muy pequeño de error.
El periodo de Grecia en el que vivió Eratóstenes, la época Helenística, abarca desde el 323 a. C., fecha de la muerte de Alejandro Magno, hasta el 31 a. C., año en Grecia y el oriente griego caen definitivamente bajo el poder de Roma.
En el orden económico hubo una decadencia generalizada de la agricultura, excepto en Egipto. La industria se estancó, pero floreció el comercio; se difundió la economía monetaria y se fundaron sociedades crediticias y mercantiles que potenciaron las relaciones económicas en el Mediterráneo.
En la sociedad. Una clase dirigente cosmopolita (griegos e indígenas helenizados) se asentó en los grandes núcleos urbanos, las poblaciones campesinas asimilaron sólo superficialmente la cultura griega dominante y mantuvieron sus costumbres y tradiciones ancestrales.
En el aspecto cultural, Atenas dejó de ser el centro más importante del mundo helénico y con ella rivalizaron Alejandría, Antioquía, Pérgamo, Éfeso y Rodas. Gracias a la iniciativa de los reyes se desarrolló una intensa actividad intelectual y científica, plasmada en la creación de bibliotecas, museos, gimnasios y teatros, y en el incremento de la ciencia especulativa y experimental. Durante estos siglos se difundió la cultura entre grandes masas de población y aparecieron nuevas formas artísticas más ricas y expresivas, indicadoras de una nueva sensibilidad para los aspectos cotidianos de la vida.
En lo religioso y moral, la desaparición de la polis como forma de organización política, acarreó la desaparición de la religión estatal. Las creencias religiosas dejaron de ser patrocinadas por el Estado y se convirtieron en asunto propio de la conciencia individual. Por otra parte, surgieron religiones universalistas, que se dirigían a toda clase de personas, religiones en las que abundaban elementos mistéricos, mágicos y supersticiosos.
Valoración personal: