Hoy es un día especial, hemos salido al patio a investigar con un palo de 1,65 cm y un metro. Nos hemos transformados en físicos y en matemáticos imitando a Tales y Eratóstenes en alguno de sus experimentos. Observemos los resultados:
TALES
Lo primero que hemos aprendido es que no es necesario subirse a los sitios para medir su altura, sino que midiendo su sombra podemos calcularla nosotros mismos. Este es un método bastante sencillo de entender, al conocer la altura del palo y la sombra que éste proyecta a una hora determinada, un día determinado y un lugar determinado (y esto es lo más importanto porque sino la sombra varía) podemos calcular la poporción entre ambos y porlo tanto conocer la proporción entre todos los objetos y su sombra. De esta manera para conocer la altura de un objeto solo es necesaio medir su sombra. Hemos hecho la experiencia con: las portería, la canasta y el colegio. En el caso de la portería, su sombra medía 3 m, por lo que su altura medirá la altura que mide el palo (1,65 m) por la sombra de la portería (3 m) entre la sombra del palo (2,34) = 2,11m. En el de la canasta a= 1,65 x 3,80 / 2,34 = 2,67 m. Y en el del colegio aplicando la misma regla de tres nos salía una altura de 7,95 m.
Aquí mostramos un gráfico que esperamos sirva para clarificar dudas:
Los dos triángulos CAB y CA´B´ son semejantes, aligual que los que formaban el palo su sombra y los rayos de sol con el resto de objetos. Esto tiene varias implicaciones: todos los ángulos son iguales, sus lados son propocionales: AB/A´B´= BC/B´C = CA/CA´= w (proporción); sus areas son proporcionales y además la razon de éstas es el cuadrado de la de sus segmentos, ya que se tratan de distintas dimensiones: AB x AC / 2 / A´B´ x A´C /2 = AB x AC / A´B´x A´C = w^2
ERATÓSTENES
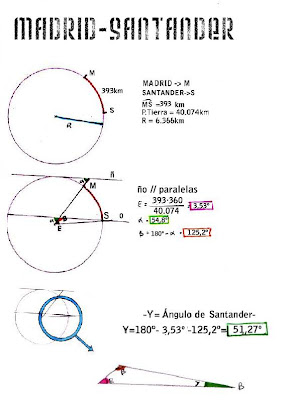
Ahora vamos a convertirnos en personas de hace más de 2.000 años y vamos a calcular los ángulos que formarían nuestro palo y su sombra, a la misma hora que realizamos nuestro experimento, en distintas ciudades que obviamente se encuentran en el mismo meridiano que Madrid. Esto no nos sería posible hace tanto tiempo porque se desconocía la longitud de la circunferencia terrestre, que es lo que en realidad calculó ingeniosamente Eratóstenes, por eso vamos a trabajar al revés que él, hallando primero el ángulo que se formaría en Burgos:
Primero hemos medido el ángulo que se forma en Madrid mediante las proporciones entre el palo y la sombra: el palo era el cateto adyacente y la sombra el cateto opuesto; así hemos calculado la tangente e introduciéndolo en la calculadora hemos hallado el ángulo (54,8). Es importante tener en cuenta que Eratóstenes no disponía de calculadora y que no utilizaba el sistema que utilizamos nosotros para medir grados sino que lo que utilizaba eran proporciones…alucinante.
Como el sol está muy lejos de la Tierra y ésta es muy pequeña comparada con él, consideramos que los rayos del sol son paralelos. De esta forma imaginemos el cruce entre el rayo del sol y una supuesta prolongación de nuestro palo que llegase al centro de la Tierra, ¡Se formaría el mismo ángulo que en la superficie! (54,8). Ahora imaginemos un triángulo con estos ángulos, el primero que fuese el que se forma con el cruce del rayo de sol que atraviesa la Tierra con nuestra prolongación, otro el que se forma con el cruce de la prolongación de nuestro palo con la prolongación del de Burgos en el centro de la Tierra y el otro con el palo de Burgos y el rayo de sol. Como se muestra en la figura:
De esta manera podemos deducir que en el triángulo que forman las tres rectas podemos hallar los tres ángulos y por lo tanto conocer el que se formaría en Burgos al que vamos a llamar Y.
Hemos de hallarla sabiendo que existe una proporción entre las distancias Madrid-Burgos entre la circunferencia terrestre y los ángulos E y 360º.
Al conocer la distancia Madrid-Burgos (237) y la de la circunferencia terrestre (40.074), podemos hallar E:
Así pues, Y= 180º- Beta – Épsilon= 52,871º
Como podréis apreciar en las siguientes figuras, Beta siempre se mantiene constante para todos los casos porque nuestro palo es fijo, en cambio Épsilon e E irán creciendo uno y disminuyendo el otro indirectamente proporcional. Siempre habrá que realizar la misma regla de tres y el mismo razonamiento. Los otros ángulos que nos han salido han sido: 51,27º (Santander), 50,902º (Granada) y 44,02º (Exeter)
He aquí los gráficos y pasos:
También hemos realizado un trabajo de investigación para conocer la relación entre el radio de la tierra y su volumen: V= 4piR^3 /3= 1,09 x 10^12 km^3
Y por último su área, que A= 4piR^2= 5,14 x 10^8 km^2








No hay comentarios:
Publicar un comentario